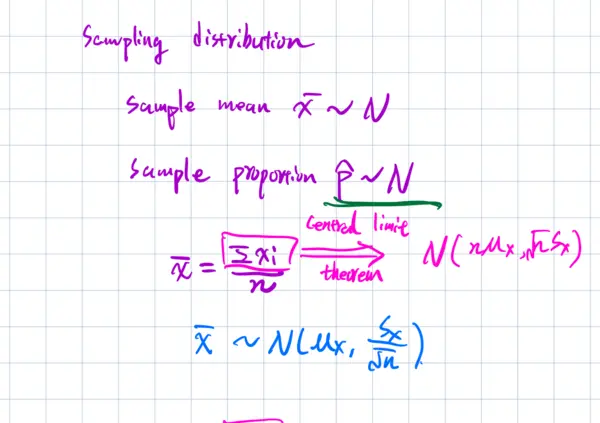
Sampling distribution Sample mean $\bar{X} \sim N$ Sample proportion $\hat{P} \sim N$ Central limit $\bar{X} = \frac{\sum x_i}{n} \implies \text{theorem} N(\mu_X, s_X)$ $\bar{X} \sim N(\mu_X, \frac{s_X}{\sqrt{n}})$ $\hat{P} = \frac{\sum x_i}{N}$ $x_i \sim \text{Bernoulli distribution}$ $\sum x_i \sim \text{Binomial}(N, P)$ $Np \ge 10, N(1-P) \ge 10 \implies$ Population proportion $\sum x_i \sim N(np, \sqrt{np(1-p)})$ $\hat{P} \sim N(P, \sqrt{\frac{P(1-P)}{n}})$ $\bar{X} \sim N(\mu_X, \frac{\sigma_X}{\sqrt{n}}) \leftarrow$ assumption: 1) SRS. $\implies$ unbias $\implies \mu_{\bar{X}} = E(\bar{X}) = \mu_X$ 2) $n \ge 30$ or $X \sim \text{Normal}$ 2.1) how to check if $X \sim \text{Normal}$ 2.1.1). sample has no skewness or no outlier. $\implies$ population is normal 2.1.2) Q-Q plot of sample is all on a straight line. 3) $n < 0.1 N_0 \implies$ independent sampling $\sigma_{\bar{X}} = \frac{\sigma_X}{\sqrt{n}}$ $\implies \text{Var}(\bar{X}) = \text{Var}(\frac{\sum x_i}{n})$ $= \frac{1}{n^2} \text{Var}(x_1+x_2+...+x_n)$ independent $\implies = \frac{1}{n^2} [\text{Var}(x_1)+\text{Var}(x_2) + \dots + \text{Var}(x_n)]$ $= \frac{1}{n^2} \times n \text{Var}(X)$ $= \frac{\text{Var}(X)}{n}$ $\sigma_{\bar{X}} = \sqrt{\frac{\text{Var}(X)}{n}} = \frac{\sigma_X}{\sqrt{n}}$ the distribution of 多个样本的分布 sampling distribution 的分布 一个样本内数据 的分布 sample distribution 敏可能班 的平均身高 一个班身高 分佈 Population distribution 一个学校 的身高分佈 3 conditions $\implies \bar{X} \sim N(\mu_X, \frac{\sigma_X}{\sqrt{n}})$ another 3 conditions $\implies \hat{P} \sim N(P, \sqrt{\frac{P(1-P)}{n}})$ 已知 $n=50$, $\hat{P}=0.47$. 求 $P$ 大致范围. population proportion $\implies$ 未知. 当符合 3 条件时, $\hat{P} \sim N(P, \sqrt{\frac{P(1-P)}{n}})$ 95% 的 $P$ 在这个范围 95% 的情况下 $P$ 在这个范围 $\hat{P} - 2\sqrt{\frac{P(1-P)}{n}}$ 0.27 $\hat{P}$ $\hat{P} + 2\sqrt{\frac{P(1-P)}{n}}$ 0.67. 6.67 + 0.64 = 1.31 $\implies$ 31% $2\sqrt{\frac{\hat{P}(1-\hat{P})}{n}} < 3\%$ $1.96 \sqrt{\frac{\hat{P}(1-\hat{P})}{n}}$ (95% $\rightarrow$ 1.96) $0.03$ $\sqrt{n} > \frac{1.96 \sqrt{\hat{P}(1-\hat{P})}}{0.03}$ $n > \frac{1.96^2}{0.03^2} \hat{P}(1-\hat{P})$ $n > \frac{1.96^2}{0.03^2} 0.5^2$ $n > 1111$ 置信区间 confidence interval. C.I. 置信度 confidence level. C-level 误差幅度. Margin of Error M.O.E. 临界值 Critical Value C.V. 标准误. Standard Error S.E. CI: Sample Statistics $\pm$ MOE. CI: Statistics $\pm$ C.V. $\times$ S.E. !!! 置信度不是概率. 4-Step process. State: 1)声明要做什么。 2) 声明细节 3) 声明使用符号指代变量 Plan: 1)声明使用方法 2)该方法所用条件. Do: 1)用计算器计算 2)写请结果 Conclude: 做结论,汇报结果 State: We are constructing a C.I. for $P$ at C-level=95% Where $P$ is the true proportion of female students in all students in our school. Plan: 1-sample Z-interval for $P$. 只抽了一个样. Sampling distri 要估计的 只给一个pop. parcam,的形态.. population Parameter. 做估计 z代表正态分布. 如果是 for $P_1-P_2$ 则是2-sample 两个proportion之差. Do. 手算 C.I.公式: Statistics $\pm$ Critical ValueX Standard Terror 用C-level算出 $\frac{1+\text{C-level}}{2}$ $\hat{P} \pm \text{invNorm}(\text{area: } \frac{1+\text{C-level}}{2}, \mu:0, \sigma:1) \sqrt{\frac{\hat{P}(1-\hat{P})}{n}}$ $0.47 \pm 1.96 \sqrt{\frac{0.47 \times 0.53}{50}}$ Do. 用计算器算. By using calculator, X: 23 n: 50 C-level: 0.95 1-PropZInt We get (0.345,0.618). Conclude: We are 95% confident that the true proportion of female student among all students in our school is between 0.345 and 0.618. Confidence interval done. Hypothesis testing. 假设 检验 当别人说一个claim.你想证明他 对or错. 1)当作claim已经成立。 2) 取样算概率. P-value 3)若p-value极小.说明不该抽到社 4)说明原假设错误 ①定假设. (1)你看到別人的claim eg. $p > 0.7$ ov $P=0.7$ 2)你同意?不同意? 你想证 $P > 0.7$ 你想证 $P < 0.7$ $H_A: P > 0.7$ 备则假设 $H_A: P < 0.7$ 将>, <或≠改为二, $H_0: P=0.7$ 原假设.$H_0: P=0.7$ 通过推翻原假设 来证明备则假设. 通过原假设成立时, 抽到了极小概率样本,但不应该 抽到极小根概率样榊 故原假设不成立 来推番羽原假資. 1) 原假设已成立. $P=0.7$. $\implies \hat{P} \sim N(0.7, \sqrt{\frac{0.7 \times 0.3}{50}})$ $P=0.47$. $P20.47$ P-value = $P(\hat{P} \le 0.47) = \text{normalcdf}(\text{lower}:0, \text{upper}:0.47, \mu:0.7, \sigma:\sqrt{\frac{0.7 \times 0.3}{50}})$ $\approx 0$ P-value < 0.05 $\implies$ 拒绝原假设. $\implies H_A$ 成立. $P < 0.7$ ①定假设。②验条件③算第一值出结论 State: ①假设是什么. ②使用的数学符号代表什么变量。 ③用$\alpha$-level Plan: ①写明使用的方法。 1-sample Z-test for $P$ ②验条件. 1) SRS 2) 10% $n<10\%N$ *3) $np \ge 10, n(1-P) \ge 10$ 这里是$P$ Do. 1)用计算器 By using calculator $P_0: 0.7$ x: 23 n: 50 props $