Class: AP2 | Unit: Unit 4 | Updated: 2026-02-09
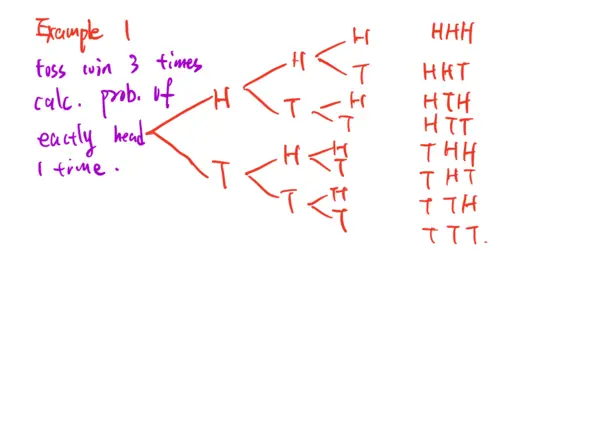
Example 1 H HHH toss coin 3 times H E(X) increases => graph shifts right. Std(X) = $\sqrt{np(1-p)}$. n increases => Std(X) increases => Std becomes larger. Graph becomes shorter and fatter. When n remains constant and p increases: E(X) = np. E(X) increases => graph shifts right. Std(X) = $\sqrt{np(1-p)}$. When $p > 0.5$, Std(X) increases. When p moves away from 0.5, Std(X) decreases. When $p \to 1$ and $n(1-p) < 10$: graph cut off on the right => skew to left. When $P \to 0$ and $np < 10$: cut off on the left => skew to right. !!! X is defined as the number of successes. Conditions for Binomial distribution: 1) fixed total number of trials n. 2) only 2 outcomes each trial. 3) fixed success prob. P. 4) independent between trials. Geometric R.V. distribution. X represents the order of first success among a series of trials. Conditions for Geometric distribution: 1) trials with only 2 outcomes (success/fail). 2) equal success prob. p for all trials. 3) independent trials that do not affect each other. X ~ Geom(p). PDF of geometric R.V. P(X=k) = $(1-p)^{k-1} p$. CDF of geometric R.V. P(X≤k) = P(X=1)+P(X=2)+.... +P(X=k). For geometric $1 \leq X \leq \infty$. E(X) = $\frac{1}{p}$. Std(X) = $\sqrt{\frac{1-p}{p^2}}$. shape: skew to the right.