Class: AP3 | Unit: Unit 4 | Updated: 2025-12-24
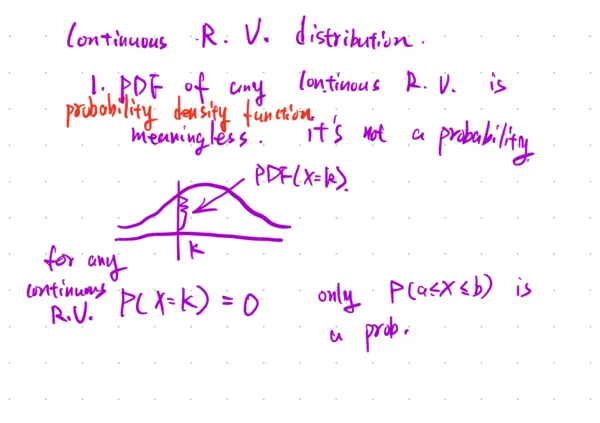
Continuous R. V. distribution.1. PDF of any continuous R. V. is probability density functionmeaningless. it's not a probabilityPDF(X=k).for anycontinuous R.V. P(X=k) = 0 only P(a≤X≤b) is a prob.2. P(a≤X≤b) ⇒ CDFCumulative distribution functionFor discrete R.V. PDF is prob.i.e. P(X=k)>0For continuous R.V. PDF is not probability. P(X=k) = 0.Special continuous R.V. distribution.1) uniform distribution X~ Uniform (a, b)Area=11/(b-a)abP(i≤X≤j) = (j-i)/(b-a).E(X)= (a+b)/2.std(x)=(b-a)/√122) normal distribution X ~ Norm (μx, σx)bell-shapeddensity curveSymmetriclower: aP(a≤X≤b) = normalcdf(lower: a, upper: b, μ: μx, σ: σx)μ, σ is a given parameter.one R.V.E(X±a) = E(X) ±a.E(kX)= kE(X).E(kX±a) = kE(X) ±a.Two R.V.E(X±Y) = E(X) ±E(Y).no condition.E(aX±bY±c)= aE(X) ±bE(Y) ±c.E(aX±bY±cZ±d) = aE(X) ±bE(Y) ±cE(Z) ±d.std (aX) = √a Std(X).Std (X+b)= Std(X)Std (aX+b) = √a Std(X).std (X ± Y) = √std²(X) + std²(Y)std(X±Y±Z) = √std²(X) + Std²(Y) + Std²(Z)Std (aX+bY+c) = √(a Std²(X) + b Std²(Y))